© Astvatsatur AMBARTSUMIAN
Résistance des matériaux (RDM)
Sollicitation simple : Traction et compression
Sommaire :
- Définition
- Essai de traction
- Étude des contraintes
- Condition de résistance
- Étude des déformations
- Relation contrainte/déformation
- Application
1. Définition :
Une poutre est sollicitée en traction simple (en compression) lorsqu’elle est soumise à deux forces axiales directement opposées, appliquées au centre des surfaces extrêmes, qui tendent à l’allonger (à la raccourcir).
Une poutre est en traction (en compression) dès que le torseur des efforts intérieurs dans (G ; x ; y ; z) s’exprime sous la forme suivante :
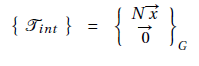
N : effort normal (effort extérieur)
Si N > 0 : traction ;
Si N < 0 : compression.
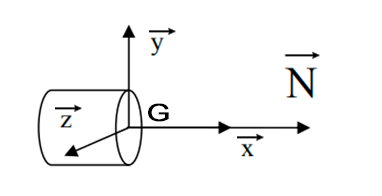
2. Essai de traction :
Fig. 1 – Machine de traction
Fig. 2 – Déformations de l’éprouvette
Fig. 3 – Courbe contrainte/déformation dans un essai de traction
![]() : contrainte normale ;
: contrainte normale ;
![]() : déformation ;
: déformation ;
– O à A : zone de déformation élastique (réversible) ;
– A à D : zone de déformation plastique répartie.
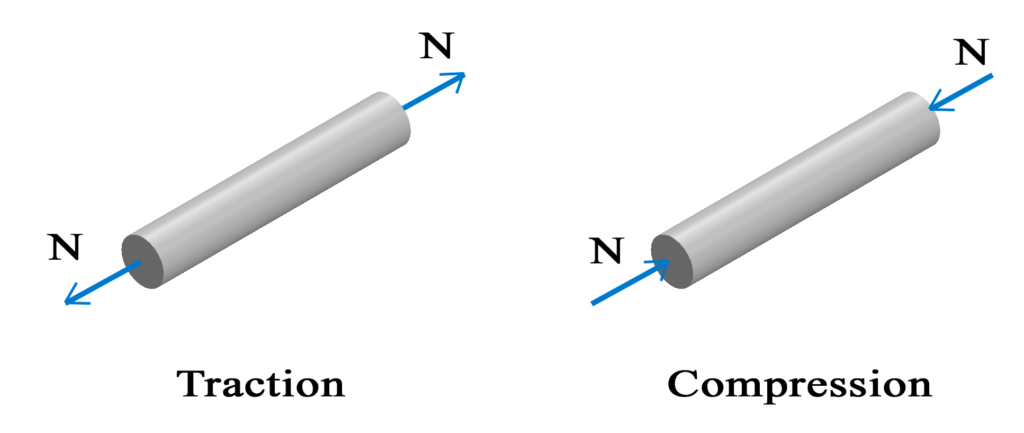
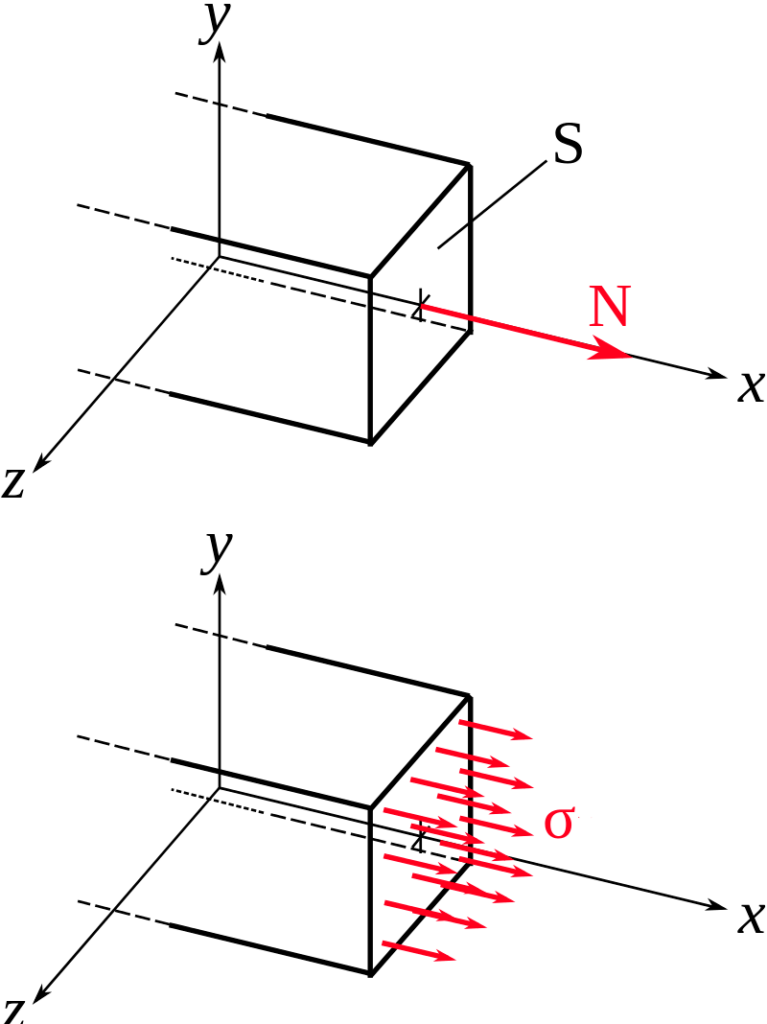
3. Étude des contraintes :
Pour une poutre, de section S, sollicitée à la traction simple la valeur de la contrainte normale est égale au rapport de l’effort normal N par la section S.
![]()
![]() : contrainte réelle de traction en tout point de la section S (
: contrainte réelle de traction en tout point de la section S (![]() ou MPa) ;
ou MPa) ;
S : aire de la section droite de la pièce (![]() ) ;
) ;
N : effort extérieur de traction sollicitant la pièce (newton, N).
4. Condition de résistance :
Afin qu’une pièce résiste aux sollicitations, il faut être certain de rester dans la zone de déformation élastique.
Pour des raisons de sécurité la contrainte doit rester inférieure à une valeur limite appelée résistance pratique à l’extension ![]() (dans le cas de la compression
(dans le cas de la compression ![]() ).
).
En général, on adopte un coefficient de sécurité s.
Tableau 1 – Coefficients de sécurité en mécanique
La condition de résistance d’une pièce en traction : ![]()
![]() , donc
, donc ![]()
![]() : résistance pratique à l’extension (
: résistance pratique à l’extension (![]() ou MPa) ;
ou MPa) ;
![]() : résistance élastique à l’extension (
: résistance élastique à l’extension (![]() ou MPa) ;
ou MPa) ;
S : coefficient de sécurité (sans unité).
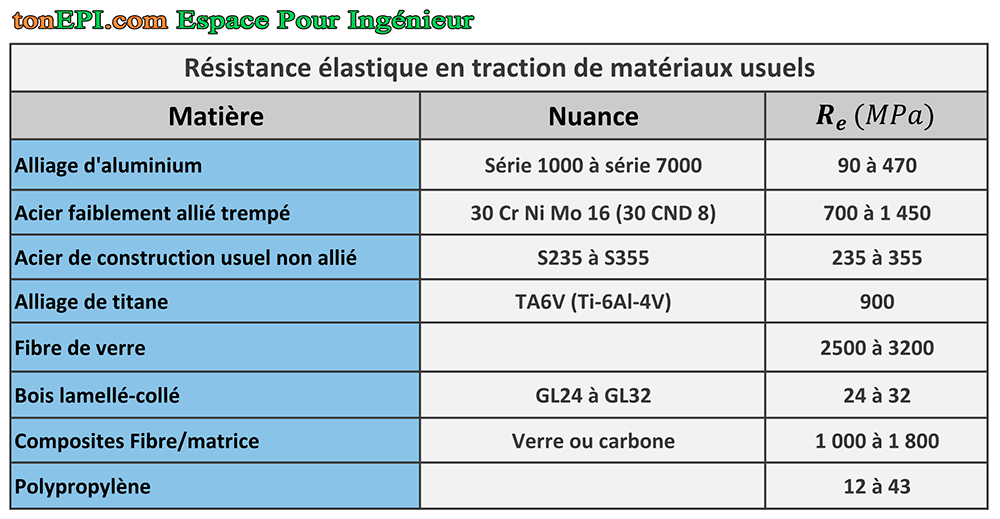
Tableau 2 – Résistance élastique en traction de matériaux usuels
Résistance élastique à l’extension ou Limite élastique ![]() :
:
Cette contrainte marque la fin du domaine élastique. Pour les valeurs supérieures, le matériau ne se déforme plus élastiquement. (Voir Fig. 3 – Courbe contrainte/déformation)
5. Étude des déformations :

On appelle déformation le rapport de la variation de longueur ![]() sur la longueur de référence
sur la longueur de référence ![]() :
:
![]()
![]() : (epsilon) allongement relatif en % ;
: (epsilon) allongement relatif en % ;
![]() : allongement
: allongement ![]() (mm) ;
(mm) ;
![]() : longueur avant déformation (mm) ;
: longueur avant déformation (mm) ;
L : longueur après déformation (mm).
La partie (OA) est la partie élastique. La pente de la droite (OA) est appelée module d’élasticité (longitudinale) ou module de Young : c’est une caractéristique du matériau que l’on notera E. La relation entre la contrainte normale et la déformation dans la zone élastique est donnée par la loi de Hooke :
![]()
E : module d’élasticité (longitudinale) ou module de Young (![]() ou MPa).
ou MPa).
La déformation longitudinale ![]() s’accompagne d’une déformation de contraction transversale
s’accompagne d’une déformation de contraction transversale ![]() .
.
Le rapport ![]() est appelé coefficient de Poisson et est noté ѵ.
est appelé coefficient de Poisson et est noté ѵ.
On a donc :
![]()
6. Relation contrainte/déformation :
![]() loi de Hooke
loi de Hooke
![]()
soit encore :
![]()
Donc, on peut également exprimer la déformation en fonction de la contrainte normale :
![]()
7. Application :
Exercice #1
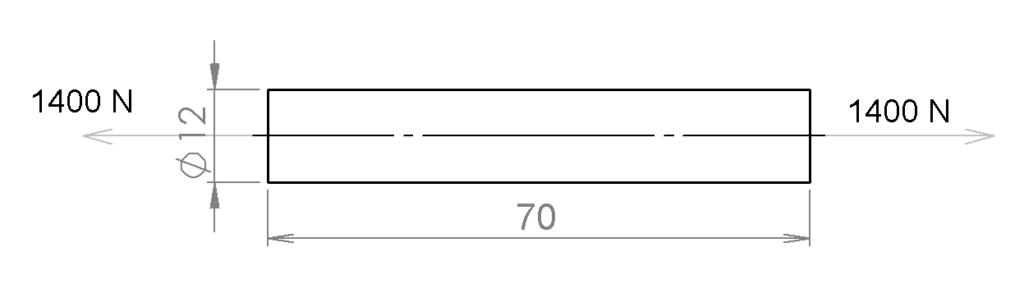
Un arbre mécanique en acier (faiblement allié) d’un tracteur de diamètre de 12 mm et de longueur de 70 mm est soumis à un effort de traction de 1400 N. Le coefficient de sécurité est : s = 7.
- Vérifier que cet arbre résiste à cette force dans des conditions de sécurité satisfaisantes.
- Déterminer son allongement.
La condition de résistance d’une pièce en traction : ![]()
![]() ;
; ![]() ;
;
![]() ;
;
s : coefficient de sécurité = 7 ;
![]() : résistance élastique à l’extension (voir tableau)
: résistance élastique à l’extension (voir tableau)
![]() = 700/7 = 100 MPa
= 700/7 = 100 MPa
On a donc :
12,38 MPa ≤ 100 MPa
Cet arbre résiste !
Maintenant, on va déterminer son allongement :
![]() ;
; ![]() : allongement (mm).
: allongement (mm).
![]()
![]() : longueur avant déformation = 70 mm ;
: longueur avant déformation = 70 mm ;
![]() : (epsilon) allongement relatif – ?
: (epsilon) allongement relatif – ?
![]() : loi de Hooke
: loi de Hooke
![]()
![]() = 12,38 MPa ;
= 12,38 MPa ;
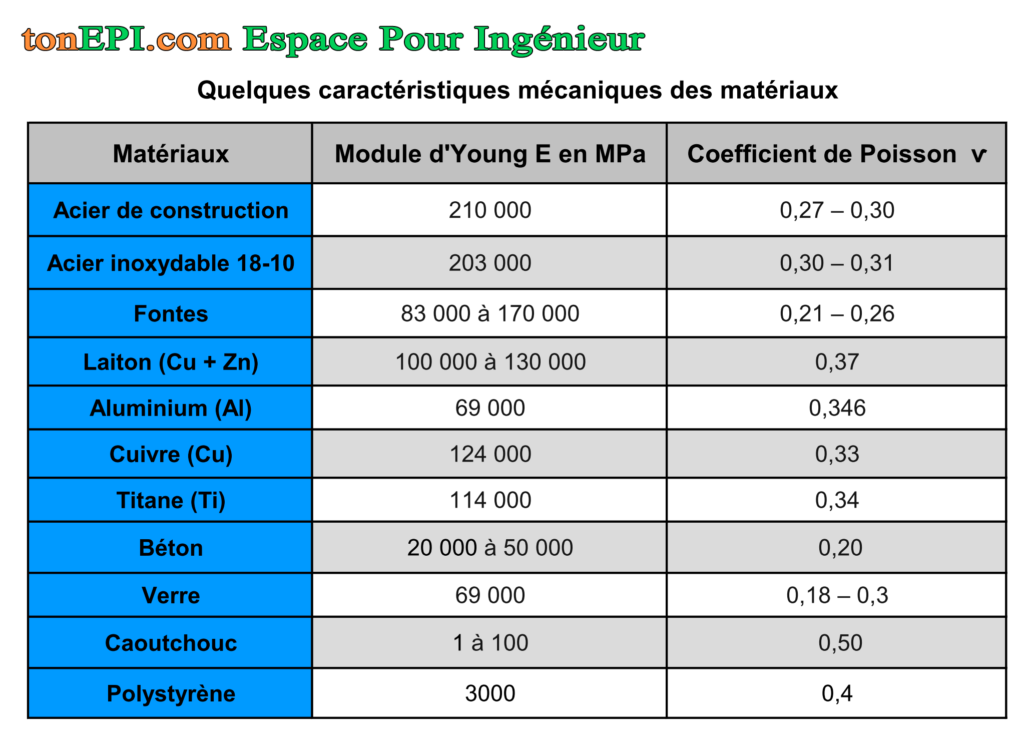
E : module d’élasticité (longitudinale) ou module de Young (voir tableau)
E = 2,1 x 105 MPa pour acier ;
![]()
![]() ;
; ![]()
Résultat :
- Arbre résiste !
- Allongement est de 0,004 mm
Exercice #2
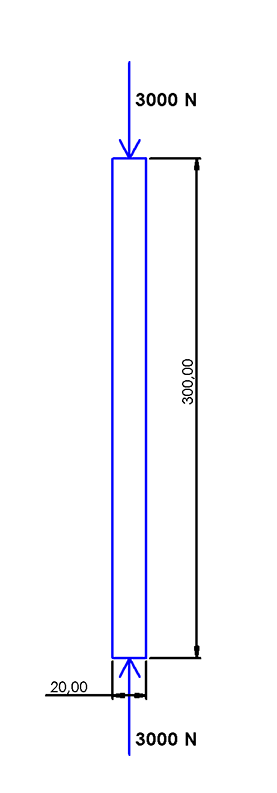
La partie AB de la construction en tube carré aluminium (20 X 20 mm, épaisseur 2 mm) est soumise à un effort de compression de 3 000 N. Sa longueur est de 300 mm. Le coefficient de sécurité est : s = 6 et la résistance élastique à la compression est : 145 MPa.
- Vérifier que La partie AB résiste à cette force dans des conditions de sécurité satisfaisantes.
La condition de résistance d’une pièce en compression : ![]()
![]() ;
;
Recherche de la section du tube carré :
S = (20 x 20) – (16 X 16) = 144 ![]() ;
;
![]() = 3000/144 = 20,83 MPa ;
= 3000/144 = 20,83 MPa ;
s : coefficient de sécurité = 6 ;
![]() : résistance élastique à la compression.
: résistance élastique à la compression.
![]() = 145/6 = 24,16 MPa
= 145/6 = 24,16 MPa
On a donc :
20,83 MPa ≤ 24,16 MPa
Résultat :
Cette partie de la construction en tube carré alu résiste !
Voir l’article : Sollicitation simple : Cisaillement







16 commentaires sur “Sollicitation simple : Traction et compression (cours)”
J’aime ce module
Merci beaucoup j’ai bien compris
Merci pour votre aide.
Toutes mes encouragements les plus cordiales
Quelle est le sens de l’axe lors de traction ?
Merci pour votre contribution
Pourquoi 16 x 16 svp à l exercice 2 ?
Épaisseur 2 mm
Moi je pens que c’est 18×18, car l’épaisseur c’est 2
Non, c’est 16×16. 2 mm de chaque côté
La partie elle est bien explicitée
Comment l’avoir en version pdf?
J’apprécie beaucoup cette plate forme
En cas de compression d’un tube, la partie creuse n’est pas à prendre en compte ou le calcul diffère?
merci beaucoup votre cour est trop bien détaillé Jai tout compris
vraiment merci encore
Merci beaucoup pour l’enseignement
Pour l’exercer n°1. Comment vous avez trouvez la valeur de π
Bonjour!
Cours très bien expliqué pour les initiés en RDM,
Merci pour le partage!