Méthode de la différence logarithmique des températures (MDLT)

Ani AMBARTSUMIAN ©

Objet : dimensionnement d’un échangeur tubulaire par la méthode de la différence logarithmique des températures (MDLT). Exemple concret de ce dimensionnement.

L’échangeur de chaleur tubulaire est un appareil sous pression à deux circuits de fluides séparés (côté calandre et côté tubes).

Fig.1 Exemple d’un échangeur tubulaire

Le dimensionnement d’un échangeur consiste à calculer la surface d’échange nécessaire pour obtenir les performances désirées (puissance, température de sortie).

La Méthode de la différence logarithmique des températures (MDLT) est l’une des méthodes de dimensionnement des échangeurs qui permet de déterminer la surface de l’échangeur et ne s’applique que dans des conditions strictes :

• le coefficient d’échange global  est supposé constant,
• les échangeurs sont à circulation parallèle (co ou contre-courant) ou corrigé d’un facteur F si ce n’est pas le cas,
• les capacités thermiques massiques des fluides sont supposées constantes tout au long du processus.

La puissance d’un échangeur P, [W] implique la notion de conservation de l’énergie entre deux fluides :

Où :

, : débit massique des fluides respectivement chaud et froid, en  ;

,  : chaleur spécifique à pression constante des fluides respectivement chaud et froid, en   ; (caractéristique de l’aptitude du fluide à absorber de la chaleur)

, : écart de température des fluides respectivement chaud et froid , en K ou en °C ;

  

,  : températures d’entrée des fluides respectivement chaud et froid, en K ou en °C  ;

,  : températures de sortie des fluides respectivement chaud et froid , en K ou en °C  ;

L’échange thermique a lieu uniquement si la différence de température entre les deux fluides est suffisante. Plus la différence de température est grande, plus la surface d’échange nécessaire à l’échange thermique sera petite.

À côté de l’équation de bilan énergétique, la résolution des problèmes d’échange thermique nécessite l’écriture d’une seconde équation :

L’équation de transfert de chaleur :

Où :

U : coefficient global d’échange de chaleur qui dépend des caractéristiques de l’écoulement et des fluides, en W/( ·K) ;

Une grande part du calcul d’un échangeur repose sur l’évaluation du coefficient d’échange global. Le coefficient d’échange global U se calcule à partir des différentes résistances thermiques de convection (interne et externe), de conduction (paroi solide) et éventuellement des résistances  d’encrassement. Il y a différentes méthodes pour calculer précisément ce coefficient. On peut aussi trouver des valeurs approximatives à l’aide du tableau ci-dessous :

Tabl.1 Ordre de grandeur du coefficient d’échange global pour des échangeurs thermiques

: Surface d’échange, en ;

: différence de température logarithmique moyenne (DTLM), en K ou en °C ;

Voir l’article : Différence de température logarithmique moyenne entre les deux fluides (DTLM)

Grâce à l’écriture de ces bilans, on peut ainsi facilement retrouver une grandeur (par exemple   ou ) si on connait l’ensemble des autres grandeurs.

Dans le cas où les échangeurs ne sont pas à circulation parallèle (c’est-à-dire, à courants croisés, par ex. des batteries à ailettes), on introduit dans l’équation de transfert de chaleur un facteur correctif F (valeur comprise entre 0 et 1) qui prend en compte la spécificité de l’échangeur.  Ainsi, la puissance thermique s’écrit : 

Le facteur correctif F est repéré à l’aide d’abaques en fonction de deux paramètres d’entrées :

Abscisse :

Courbes :

Où :

,: températures respectivement d’entrée et de sortie du fluide côté « Tube », en K ou en °C  ;

,: températures respectivement d’entrée et de sortie du fluide côté « Enveloppe », en K ou en °C  ;

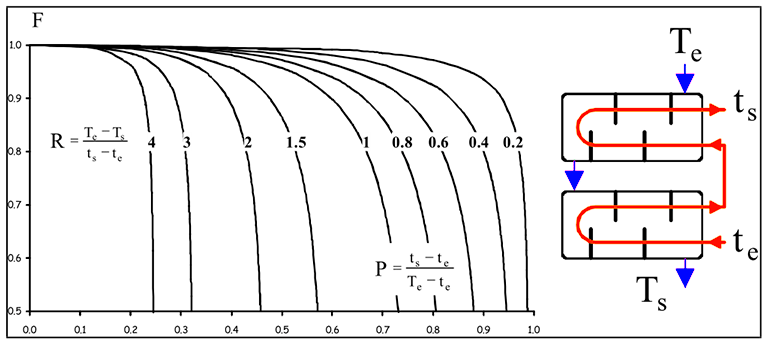
Fig.2 Abaque pour trouver le facteur de correction F d’un échangeur constitué d’une calandre et d’un multiple de 2 passes de tubes

Fig.3 Abaque pour trouver le facteur de correction F d’un échangeur constitué de 2 calandres et d’un multiple de 2 passes de tubes

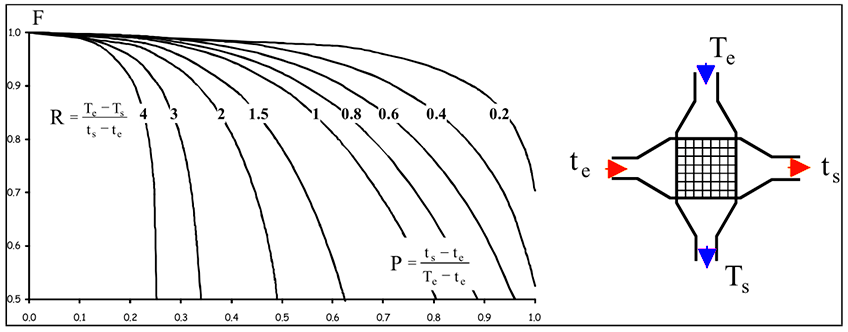
Fig.4 Abaque pour trouver le facteur de correction F d’un échangeur à courants croisés, aucun fluide n’étant mixé

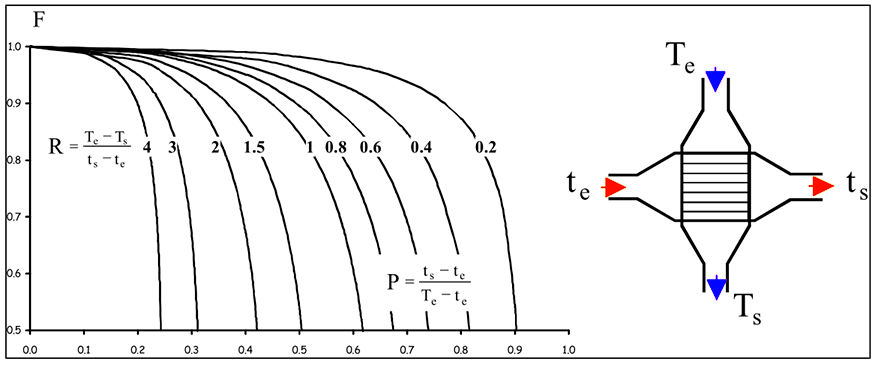
Fig.5 Abaque pour trouver le facteur de correction F d’un échangeur à courants croisés, seul l’un des fluides étant mixé

Dans le cas où les températures de sortie sont connues, le calcul d’un échangeur par la méthode de la différence logarithmique des températures (MDLT), consiste à :

 Calculer la puissance de l’échangeur P, [W] par le bilan énergétique :

Calculer la différence de température logarithmique moyenne :

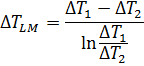
Déterminer la surface d’échange S par l’équation de transfert de chaleur :

On en déduit :

Dans le cas d’échangeur à co ou contre-courant  . Sinon, on détermine F à l’aide d’abaques.

Dans le cas où les températures de sortie sont inconnues :

Dans ce cas-là la surface d’échange S et les températures d’entrée des fluides sont connues.

On trouve les températures de sortie des fluides par la résolution complexe du système d’équations :

---

Exemple du dimensionnement d’un échangeur de chaleur par la méthode de la différence logarithmique des températures (MDLT)

À l’aide de l’exemple suivant vous allez voir comment déterminer l’aire d’échange nécessaire pour un échangeur à co et contre-courant.

Exemple : 15 T/h d’huile s’écoulant dans un tube est refroidie de 100 à 45 °C par de l’eau liquide passant de 20 à 35 °C. Le coefficient global d’échange U est égal à 300 W/( ·K). Calculer l’aire d’échange nécessaire pour un échangeur à contre-courant et co-courant.

Les données des fluides

Eau :

Masse volumique 992  

Chaleur Spécifique 4185 

Huile :

Masse volumique 902 

Chaleur Spécifique 1520 

Solution de l’exemple :

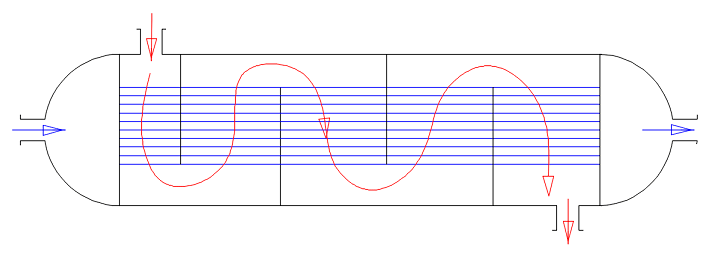
Avant tout, il serait très utile de représenter schématiquement l’échangeur à co et contre-courant (c’est-à-dire signaler où se trouvent les deux fluides avec leurs valeurs de température).

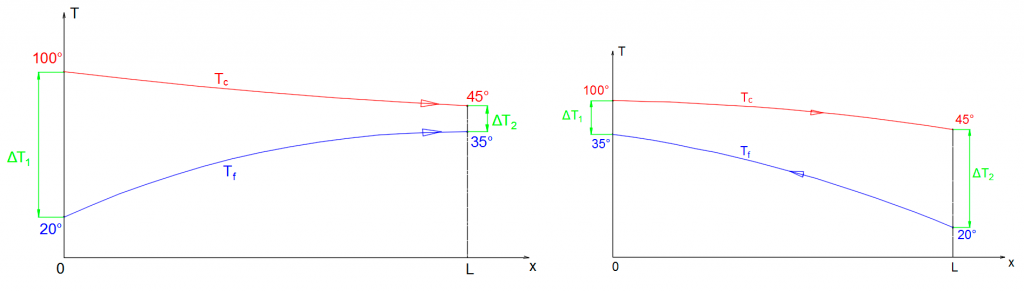
Fig.6 Représentation schématique de l’échangeur à co et contre-courant

Comme les températures de sortie sont connues, on calcul tout d’abord la puissance de l’échangeur P, [W] par le bilan énergétique :

Le débit massique de l’huile s’exprime dans le système S.I. () :

L’écart de température du fluide chaud est :

La puissance de l’échangeur est donc égale à :

On détermine l’aire d’échange nécessaire S par l’équation de transfert de chaleur :

L’expression de l’aire d’échange S peut alors être écrite sous la forme suivante :

On définit la différence de température logarithmique moyenne  pour un échangeur fonctionnant à co-courant et contre-courant :

Co-courant :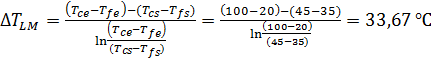

Contre-courant :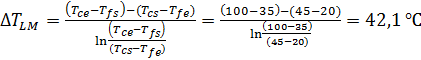

On peut donc calculer l’aire d’échange nécessaire pour un échangeur à co-courant :

On calcule l’aire d’échange nécessaire pour un échangeur à contre-courant ainsi que pour un à co-courant :

Les résultats :

Co-courant : 

Contre-courant :