Astvatsatur AMBARTSUMIAN ©
Exemple № 1 : Déterminer les dimensions limites d´un arbre ø60g11.
1. ø60g11 ( 50…60…80). Palier de dimensions nominales: 50 à 80 mm. (du tableau 1)
2. ø60g11 (11 = IT11). Tolérance fondamentale = 190 µm. (du tableau 1)
NOTE: Pour mémoire : 1 mm = 1000 µm = 0,001 m
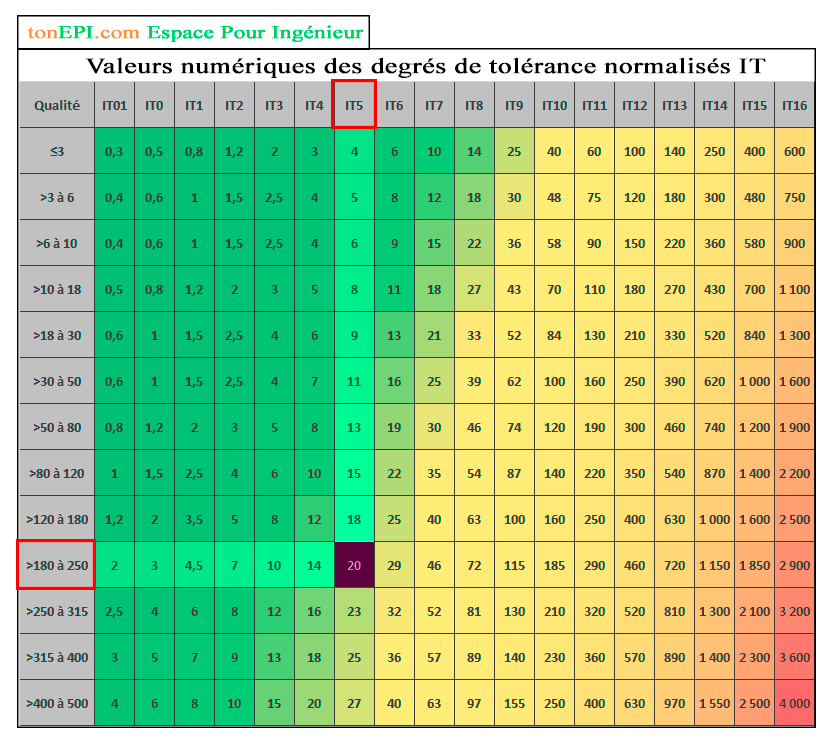
Tableau 1. Exemple de détermination de la tolérance fondamentale
Voir le tableau : Valeurs numériques des degrés de tolérance normalisés IT
3. Arbre ø60g11. Écart fondamental = – 10 µm (du tableau 2)
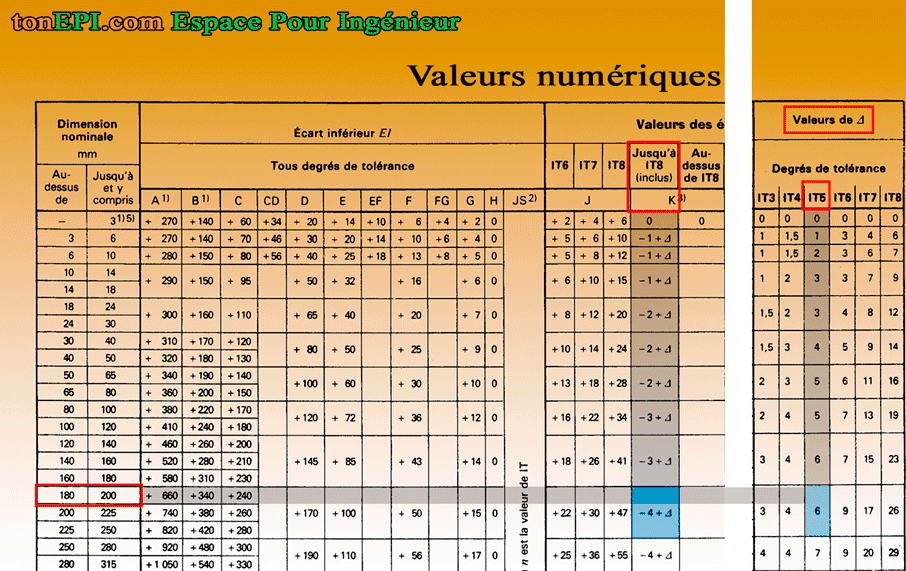
Extrait du tableau 2. Exemple de détermination de l’écart fondamental d’un arbre
Voir : Tableau 2. Valeurs numériques des écarts fondamentaux des arbres
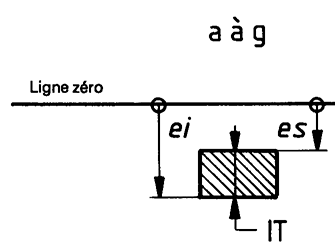
Fig. 1 Représentation schématique des positions (a à g) des écarts fondamentaux
NOTE : ei = es – IT, ou es =ei + IT
Voir aussi : Représentation schématique des positions des écarts fondamentaux
4. Écart supérieur (es) = écart fondamental = – 10 µm
5. Écart inférieur (ei) = écart fondamental – tolérance = – 10 – 190 µm = – 200 µm
6. Dimensions limites :
6.1 Dimension maximale = 60 + (- 0,01) = 59,99 mm
6.2 Dimension minimale = 60 + (- 0,20) = 59,80 mm
Exemple № 2 : Déterminer les dimensions limites d´un alésage ø200K5.
1. ø200k5 ( 180…200…250). Palier de dimensions nominales: 180 à 250 mm. (du tableau 3)
2. ø200k5 (5=IT5). Tolérance fondamentale = 20 µm. (du tableau 3)
Tableau 3. Exemple de détermination de la tolérance fondamentale
3. Alésage ø200K5. Écart fondamental = -4 + ∆ µm , valeur de ∆ = 6 µm (du tableau 4)
Extrait du tableau 4. Exemple de détermination de l’écart fondamental d’un alésage
Voir : Tableau 4.Valeurs numériques des écarts fondamentaux des alésages
NOTE : EI = ES – IT, ou ES =EI + IT
4.Écart supérieur (ES) = écart fondamental = -4 + 6 = 2 µm
5.Écart inférieur (EI) = écart fondamental – tolérance= 2 – 20 µm = -18 µm
6.Dimensions limites :
6.1 Dimension maximale = 200 + 0,002 = 200,002 mm
6.2 Dimension minimale = 200 + (- 0,018) = 199,982 mm